A expected solution to a simple problem

Intuition

Consider the unary languages of the form $L = \{1^{f(n)}\}$, exactly for what $f$ is this language regular? Intuitively, by the pumping lemma, you may end up with some $1^{f(n) + (i-1)b}$ where if $f(n) + (i-1)b$ has the same defined property as $f(n)$. For example, $1^*$ can be pumped, but $1^{n^2}$ cannot, because as you pump, you are not guaranteed that the length added will be a square. It would seem that those languages which are pumpable must have this semi-linear like property. After searching a long time for an answer, I found one.

A language is unary and regular if and only if it is the finite union of languages whos elements have lengths which follow an arithmetic progression, and a finite language.

Proof

$(\impliedby)$ The reverse direction is easier, so lets begin. Suppose we have a union of the form $\begin{equation}L_{a_1,b_1} \cup ... \cup L_{a_k,b_k} \cup L_f\end{equation}$ where $L_f$ is finite, and each $L_{a,b} = \{1^{an+b} ~|~ n \in \mathbb{N}\}$. Finite languages are regular. Each arithmetic progression language is regular because there exists the regex $L_{a,b} = L((1^a)^*1^b)$. Finally, we have a finite union of regular languages, so by closure, our language is regular.

$(\implies)$ This direction is trickier. Suppose we have a unary regular language. Then there exists a DFA for it. A DFA over a unary alphabet has much more limited structure than a general DFA. Representing the DFA as a directed graph, the unary DFAs are the directed graphs with outgoing degree one, which are strongly connected. They have $n$ vertices, and exactly $n$ edges. Although it might be hard to prove, intuitively, these graphs can only look like one thing.

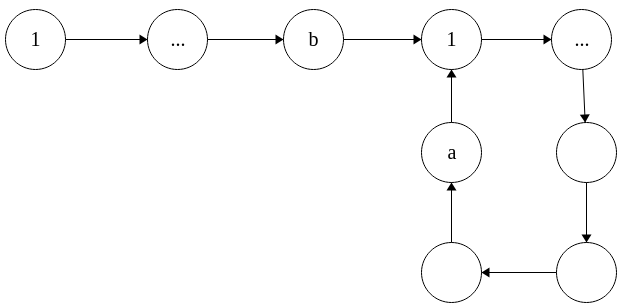
You have some tail of length $b$, followed by a loop of length $a$. Consider some computation from the start state. As you go from state to state, you can either go to a new state you have not seen before, or one that you have. If its one you haven’t seen before, great. If its one that you have, then you cannot go anywhere else since the state has outgoing degree one. Every state after must be the ones you have seen.

To get from this shape to our large union depends on the selection of final states. For each final state only on the tail, we add one word of appropriate length to $L_f$. For each final state on the loop of length $a$, of distances $b \leq c_1,...,c_k \leq a+b$ from the start state, we see that words which land on these states have lengths $an + (b + (c_i)), n \geq 0$. We associate the words which land on one state as the infinite language $L_{a,b+c_i} = (1^a)^*1^{b+c_i}$. The union of all of these sets is exactly the set of accepted strings, and the result follows.

Final thoughts.

I gave this problem to my students this semester, and most people seemed to get it, with enough time. Given just the statement, its not hard to figure out the rest, but starting with just trying to characterize the unary regular languages requires some trial and error. Someone mentioned they have found a solution for the forward implication by transforming a regular expression to the desired form of a union of kleene stars. I am not sure if this is possible just within the calculus of a regular expression, but the spirited idea is there. I am also curious if there is a solution to a similar problem in grammars. The first corollary of Parikh’s theorem is that every every unary context-free language is also regular. I wonder if there is a way to prove this without using Parikh’s theorem. Something like transforming a unary CFG to a regular grammar, in such a way which could not work for all CFGs. That might just end up looking like a special case of Parikh’s theorem, kind of like this proof does.