Puzzle cubes are cool because its like holding a real algebraic object in your hand.

When I watch people play with their puzzle cubes, I notice if they want to test the turn speed or the corner cutting or whatever, they will do these four moves (URU’R’), and repeat it six times and it will come back to the original state. That way if you want to turn it you don’t actually have to try to solve it. Another thing I noticed was if you take any face and turn it four times, you also get back to the original state. The immediate question I had was, given any list of moves, could you repeat that list and would you guarantee to come back to the original state? Playing around with it, the answer seemed true. I thought about this problem for a really long time before I came up with this proof one day during a nap.

The proof idea is to come up with some notation and rules, then form a contradiction to break those rules. A puzzle has some number of actions you can perform on it. The classic rubiks cube has twelve. Each state of the cube can be defined as a word of actions in which applied to the solved state, will induce that specific state.

• rule 1: actions are invertible. This is true because each action itself is invertible. If our actions are $a_1,a_2,a_1^{-1},a_2^{-1}$ and our state is defined by the word, say $a_1a_2a_1$, then the inverse of this state is simply $(a_1a_2a_1)^{-1}$ = $a_1^{-1}a_2^{-1}a_1^{-1}$. This makes sense intuitively. If you can move from the identity state to some state, you can also move from that state back to the identity state.

• rule 2: actions are deterministic. This should also be simple to understand. If you are at some state $A$, and you apply some actions to reach state $B$. Any time you are at state $A$ and you apply those actions, you should always reach state $B$. It really makes you think what a probabilistic puzzle might look like.

• rule 3: The number of states are finite. You can hold the puzzle in your hand, and it has a finite amount of pieces. Each state puts those pieces in a finite amount of places.

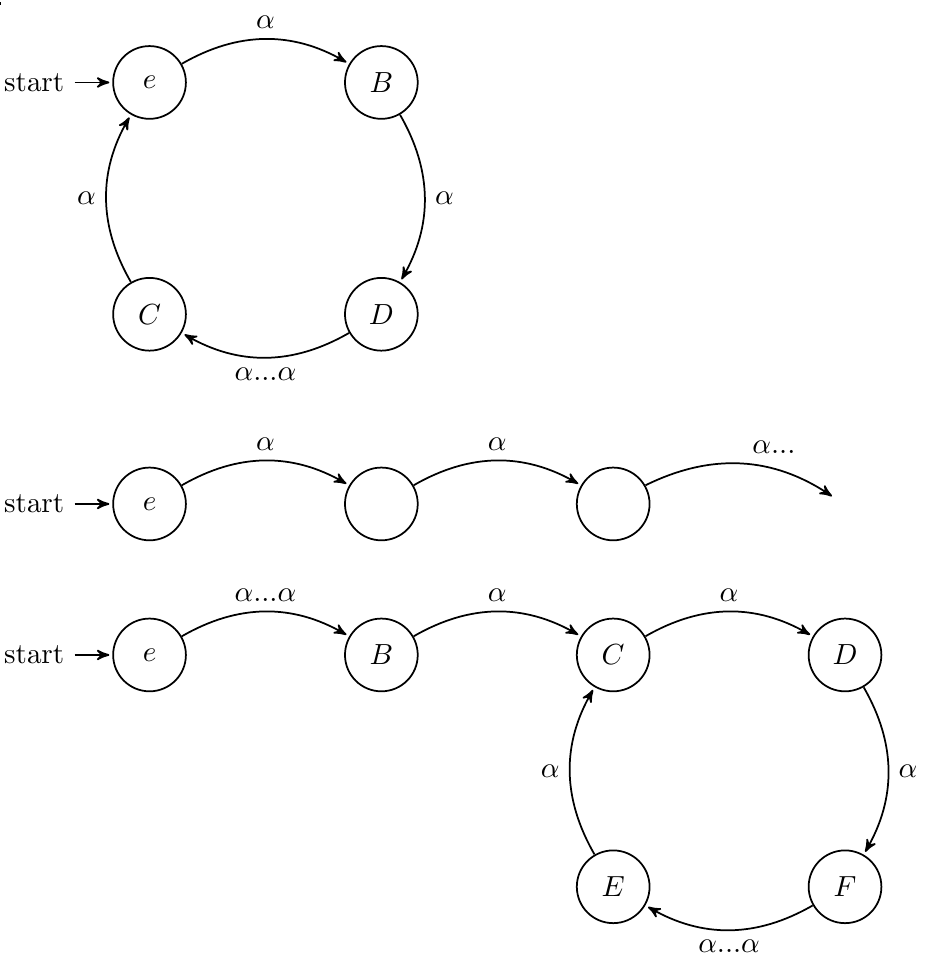
We now construct some state machines. Begin at the identity, and assume to the contrary there exists some word of actions, $\alpha$, such that no matter how many times $\alpha$ is applied, you will never return to the identity state. As we apply $\alpha$ to the identity, there exist three possible state machines:

• Case 1: This cannot be true because we assumed that $\alpha$ can never return us to the identity state

• Case 2: We assumed that there are a finite amount of states, so eventually we must return to some state we have visited before. We cannot just go on forever.

• Case 3: Since $\alpha$ has an inverse, we can also construct a state machine for $\alpha^{-1}$. Using the same states as before, we have this segment:

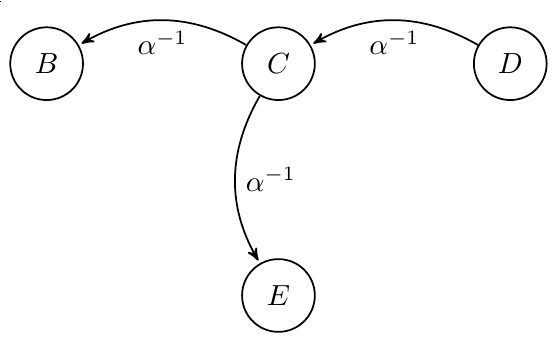
However, actions must be deterministic and this is clearly not! state $C$ goes to both state $B$ and $E$ under $\alpha^{-1}$. Therefore, every state machine of a word is a cycle. Repeated a finite number of times, every word will return to the identity.

I showed this proof idea to a postdoc and he told me an even easier proof that can be found in the first chapter of every single group theory book. The first proof was with state machines, this proof is with group theory, but the idea behind them is the same.

The words that define states of our puzzle form a group, (with the moves as generators). The identity word is the identity state. Each word has an inverse, and we have closure under the operation of concatentation. For $\alpha$ any group element, Consider the list $\alpha,\alpha^2,\alpha^3,...$ and notice that this list is infinite. Each element in the list corresponds to a state, of which we know there are finitely many of. There are two elements in this list that are equal. Let these be $\alpha^n$ and $\alpha^m$. We know that $\alpha^m = \alpha^n$. Since we have the cancellation property, then we see that $\alpha^{m-n} = e$. What this says is that applying $\alpha$ to the identity state $m-n$ times, we will return to the identity state. Or how its phrased in textbooks, all elements of a finite group have an order.

I want to make some remarks on these proofs. First, notice that the result is completely independent of the geometry of the puzzle. This will work on a cube, a megaminx, anything that satisfies our three rules. This problem was in the back of my mind for over a year. I was trying to attack it using combinatorics, when there was a very easy group theorectic way. All it took was a change of perspective. I got the idea for the first proof while reading t’Hooft’s cogwheel model (specifically section 7.1) where he tries to formulate a deterministic model of quantum mechanics.